Dérivation, fonctions et courbes 171 exercices corrigés

Description

Maîtrisez la dérivation et les fonctions avec 171 exercices.

Sommaire

Recueil d’Exercices et Aide-Mémoire sur l’Analyse Mathématique

L’ouvrage Mathématiques Dérivation, Fonctions Et Courbes. 171 Exercices Corrigés, Rappels De Cours est un manuel de mathématiques. Il se concentre sur des thèmes clés de l’analyse : la dérivation, les fonctions et l’étude des courbes. Les auteurs sont Jean-Paul Margirier et C. Vadot. Ce titre est essentiel pour les recherches sur les exercices corrigés dérivation, les fonctions et courbes mathématiques et les livres Vuibert mathématiques.

---

Pratique Intensive avec 171 Problèmes Entièrement Corrigés

Ce manuel offre une opportunité de pratique significative. Il contient 171 exercices dont les solutions sont intégralement fournies. Cette quantité permet une acquisition solide des mécanismes. La présence de corrigés détaillés est idéale pour l’autonomie de l’étudiant. Il est pertinent pour l’étude des mathématiques supérieures et la préparation aux examens.

---

Rappels de Cours Structurés pour la Consolidation Théorique

En plus des exercices, le livre inclut des Rappels de Cours. Ces synthèses théoriques consolident la compréhension. Ils permettent de revoir rapidement les définitions et théorèmes essentiels. L’ouvrage est un outil précieux pour les étudiants en classes préparatoires scientifiques. Il couvre les bases de l’analyse mathématique.

---

Édition Fiable pour la Filière Scientifique (1997)

Ce manuel au format broché s’étend sur 179 pages. Il a été publié le 10 septembre 1997 par les éditions Vuibert. Vuibert est un éditeur de référence dans l’enseignement supérieur scientifique. L’ISBN 9782711724765 identifie cette ressource. Elle est indispensable pour la maîtrise des concepts de la dérivation et des fonctions.

---

Caractéristiques

• Titre : Mathématiques Dérivation, Fonctions Et Courbes. 171 Exercices Corrigés, Rappels De Cours

• Auteurs : Jean-Paul Margirier, C. Vadot

• Éditeur : Vuibert

• Format : Broché, 179 pages

• Date de parution : 10 septembre 1997

• ISBN-13 : 9782711724765

• Thème : Mathématiques, Dérivation, Fonctions, Analyse

Table des matières

Chapitre I • Continuité des fonctions

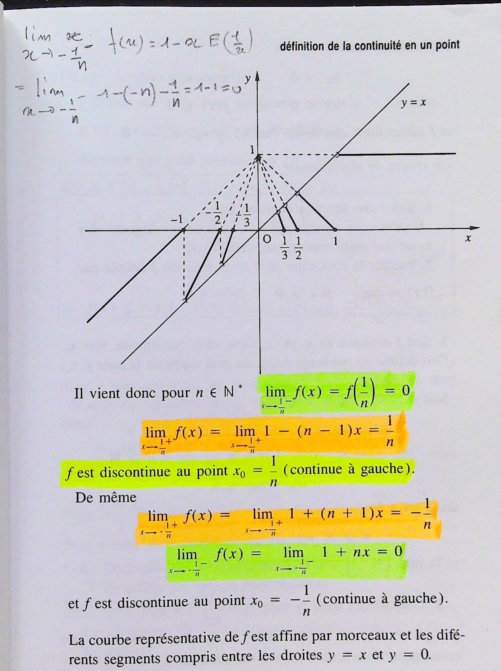
I.1. Définition de la continuité en un point ••• 5

I.2. Continuité sur une partie de R\mathbb{R}R ••• 5

I.3. Théorème des valeurs intermédiaires ••• 11

I.4. Continuité et monotonie ••• 17

I.5. Équations fonctionnelles ••• 19

Chapitre II • Dérivation

II.1. Calcul des dérivées ••• 25

II.2. Exercices divers ••• 30

II.3. Théorème de Rolle et des accroissements finis ••• 37

Chapitre III • Applications de la dérivation

III.1. Formule de Taylor ••• 45

III.2. Variations, extremums d’une fonction ••• 51

III.3. Équations – Existence de racines ••• 57

III.4. Fonctions convexes ••• 60

Chapitre IV • Développements limités

IV.1. Techniques de calcul ••• 67

IV.2. Exercices et applications divers ••• 74

Chapitre V • Fonctions usuelles – Fonctions réciproques

V.1. Fonctions réciproques des fonctions circulaires ••• 83

V.2. Fonctions hyperboliques ••• 93

V.3. Fonctions réciproques des fonctions hyperboliques ••• 101

V.4. Études diverses de fonctions ••• 107

Chapitre VI • Fonctions vectorielles

VI.1. Dérivation des fonctions vectorielles ••• 115

VI.2. Applications géométriques de la dérivation ••• 122

VI.3. Étude de courbes définies par une représentation paramétrique ••• 129

VI.4. Étude de courbes définies en coordonnées polaires ••• 142

Chapitre VII • Fonctions de plusieurs variables réelles

VII.1. Limites et continuité ••• 153

VII.2. Dérivées partielles ••• 154

VII.3. Équations aux dérivées partielles ••• 161

VII.4. Fonctions homogènes ••• 165

VII.5. Formule de Taylor, extremums ••• 167

VII.6. Différentielles – Formes différentielles exactes ••• 172

Par Jean-Paul Margirier, C Vadot

Envoi soigné et Déposé en 48h (jours ouvrables) Edition Vuibert 13 x 17,5 x 1,0 cm 168 pages Dépot légal:1990 Bon état : surlignage pages 60 ,61, 8,9,5